マルチエージェント経路計画の紹介

グラフ上の複数エージェントに対し, 互いに衝突のない経路を計算する問題は マルチエージェント経路計画 (Multi-Agent Path Finding; MAPF) と呼ばれる. MAPF はロボット群による倉庫内での荷物搬送など, 多数の魅力的な応用があり, 2010年代前半から人工知能・ロボティクス分野で盛んに研究が行われている. 本記事は日本語のチュートリアルを提供する.

お断り: 正確な話をすることが目的ではないので, 多少の不備には目を瞑ってほしい.

問題定義

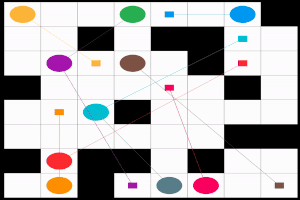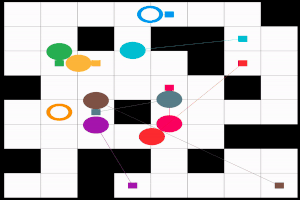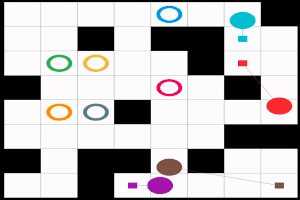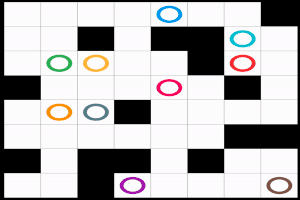
まずは, どのような問題が対象か, はっきりさせておこう. 文献によってバリエーションがあるのだが, 基本的なフォームは次の通り.

MAPF 問題はグラフ $G=(V, E)$, エージェントのチーム $A= \lbrace 1, 2, \ldots, n\rbrace $, 各エージェント $i \in A$ に対して重複のないスタート地点 $s_i \in V$ とゴール地点 $g_i \in V$ (つまり $i \neq j$ ならば $ s_i \neq s_j$ かつ $g_i \neq g_j$) で定義される. このとき, 衝突のない経路の組合わせ, つまり解 $\pi$ を求めたい.

具体的に, 解 $\pi: A \times \mathbb{N}_{\geq 0} \mapsto V$ は時刻 $t \in \mathbb{N}_{\geq 0}$, エージェント $i \in A$ をグラフの頂点 $v \in V$ に割当てる. 以下, 多くの文献にならって $\pi_i [t]$ という記法を使うことにしよう. 当然, エージェント $i$ はスタート地点 $s_i$ から移動を開始して, いつかゴール地点 $g_i$ に辿り着かなければならない. したがって $\pi$ は $\pi_i[0] = s_i$ と, 終了時刻 $t_{\text{fin}} \in \mathbb{N}_{\geq 0}$ が存在して $t \geq t_{\text{fin}}$ ならば $\pi_i[t] = g_i$ という, 二つの条件を満たす必要がある. また, $\pi$ には衝突が含まれてはいけない. 衝突にはグラフ $G$ の頂点上での衝突 $\pi_i[t] = \pi_j[t]$ と, すれ違いの衝突, つまりエッジ上での衝突 $\pi_i[t] = \pi_j[t + 1] \land \pi_i[t+1] = \pi_j[t]$ がある.

我々は任意の解に興味があるわけではなく, 一般に “良い” 解に興味があるので, 解 $\pi$ に対してコスト関数を考えよう. といってもどのような解が良いのかはアプリケーション依存である. ここでは, エージェント $i$ の経路 $\pi_i = (\pi_i[0], \pi_i[1], \ldots )$ に対するコストを $cost (\pi_i)$ と抽象化しておき, 例えばゴール地点に到達した時刻や移動距離を表すものとする. そして, エージェントのチームに対する操作 $\sum_{i \in A} cost (\pi_i)$ や $\max_{i \in A} cost (\pi_i) $ によって解 $\pi$ のコストを定義することにしよう. もちろんコストを最小化する解を見つけることが理想である.

上記は広く使われている設定だが, あくまで一例である. 例えばどのように衝突を定義するかにも色々あり, 詳しくは [Stern+ SoCS-19] を参照のこと.

なぜ魅力的な問題なのか

MAPFのキラーアプリケーションはファクトリーオートメーション, とりわけ複数のAGV (Automated Guided Vehicle) による荷物運搬である.

Ross D. Franklin / AP Photo; source

ここで, 各 AGV は荷物 (タスク) を指定された目的地へ運ぶ必要がある. 当然, AGV 同士は衝突を避けなければならないし, また, 互いに進路を妨害する立ち往生の状態, いわゆるデッドロックに陥ってはならない. また, システム全体のパフォーマンス, 例えば単位時間あたりのタスク完了数 (スループット) を最大化したいという要望があるため, 効率的な AGV 群の協調動作を計算する必要がある.

では現状の典型的なシステムがどうやって動いているかというと, ¹

1. タスクプランナーがロボット $i$ (ここではエージェントと同義) にタスクを割当て,
2. 他のエージェントを (ほぼ) 無視して エージェント $i$ の最短経路 $\pi_i$ を計算し,
3. エージェント $i$ を経路 $\pi_i$ に従って動作させる,

といった具合だ.

衝突回避は交差点に対する信号機の要領で中央集権的に行うか, もしくは自律分散的にエージェント自身がスピードを調整して, その場その場で防ぐという, 二つのやり方がある. ただどちらの方法にせよデッドロックは防ぎようがなく, 発生したら人手で解消する, というのが現状だ. この素朴なやり方だと, 衝突・デッドロック・混雑によるパフォーマンス低下などのリスクを回避するため, スペースあたりに導入するエージェントの数を保守的にする必要があることにも注意したい. つまり, 最大のパフォーマンスを得ることはできない.

一方, MAPF を解く “便利な” アルゴリズムが存在すれば, MAPF を定期的に解き続けることで, 衝突やデッドロックといったリスクを最小限に抑えることができる. それだけでなく, システムのスループットを飛躍的に向上させることができるし, より大規模なエージェント群を展開することも可能になる [Varambally+ SoCS-22]. とりわけ数百, 数千台規模のエージェント群を稼働させたい工場だと, この効果は絶大だ. つまり, MAPF は莫大な利益を生む問題になりうるのである.

ここまで物流倉庫の自動化を魅力的なアプリケーションとして紹介してきたが, より一般に, 複数の物体を効率的に移動させたいという要望は MAPF を解くことに帰着する. 夢のありそうな例を挙げると,

• 複数自動運転車の交差点管理 [Dresner+ JAIR-08] や自動駐車 [Okoso+ ITSC-19]
• 複数ロボットによる3Dプリンティング [Zhang+ Nature-22]
• 貨物鉄道運送のスケジューリング [Laurent+ NeurIPS-Comp-20]
• ドローンショーなどの小型ロボット群による情報提示 [Le Go+ UIST-16]

などは, そのようなマルチエージェントシステムの構造を内包している. ここ見るように, MAPF は近未来の高度なオートメーション化の実現に鍵となる技術 である.

どうやって解くか

それでは, この魅力的な MAPF をどのように解いていくか, 概観していこう.

A* の適用

実は MAPF はシングルエージェントの経路計画に還元できる. したがって最も素朴なアプローチは, 著名な A* アルゴリズム [Hart+ 68] を MAPF に適用することだ. まずはこれを確認しよう.

MAPF において, すべてのエージェントの位置を決めると, システムの状態が定まる. これを 構成 と呼ぶことにして, $Q \in V^{|A|}$ で表記する. ここで $V$ はグラフ $G$ の頂点, $A$ はエージェントのチームを表すことを思い出してほしい. 例えば, エージェント $i$ のスタート地点 $s_i \in V$ とゴール地点 $g_i \in V$ を用いると, システムのスタートの構成は $\mathcal{S} := (s_1, s_2, \ldots, s_n)$, ゴールの構成は $\mathcal{T} := (g_1, g_2, \ldots, g_n)$ と表すことができる.

次に, ある構成 $Q = (v_1, \ldots, v_i, \dots, v_n)$ が与えられたとき, エージェント $i$ を $v_i$ から隣の頂点 $v’_i$ に移動させることを考える. このとき, $j \neq i$ に対して $v’_i \neq v_j$ であれば, エージェント $i$ は衝突なしに $v’_i$ に移動することができ, 結果として別の構成 $Q’ = (v_1, \ldots, v’_i, \ldots, v_n)$ が生まれる. つまり $Q$ から $Q’$ へとシステムの構成を遷移させることができる. 衝突がない限りはエージェント $i$ だけでなく, 複数のエージェントを同時に動かすこともでき, このようにして $Q$ から遷移可能な構成を列挙することができる. ちゃんと言うと, グラフ $G$ の最大次数を $\Delta$ として (グリッドであれば $\Delta = 4$), 一つの構成からは $O\left( (\Delta + 1)^{|A|} \right)$ 個の遷移可能な構成が存在する.

さて, 新しい構成 $Q’$ からも同様に遷移可能な構成を列挙できることを踏まえると, 構成ひとつひとつを頂点として, 遷移可能な構成のペアに辺を導入することで, 巨大なグラフ $H$ を作ることができる. すると MAPF は開始頂点を $\mathcal{S}$, 目標頂点を $\mathcal{T}$ としたグラフ $H$ 上ので経路計画問題になる. つまり単なるシングルエージェントの経路計画なので, 下図のようにして, A* アルゴリズムを直接適用することができる.

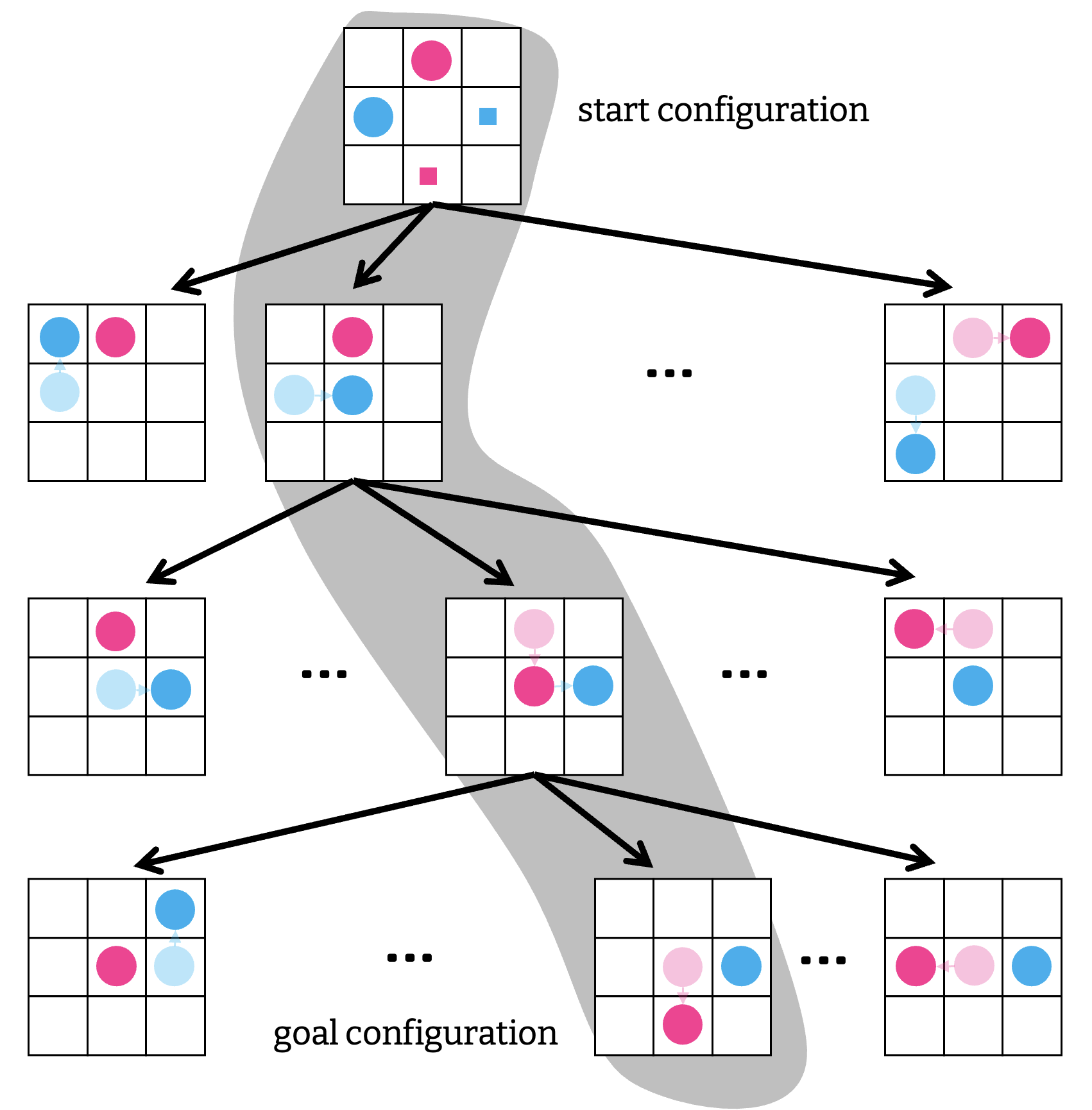
エージェントを ○, ゴールを□で表した.

残念ながら, これで問題が解けたとそう簡単な話でもない. 一般にマルチエージェントシステム・マルチロボットシステムにおいて重視されるのは, エージェント数 $|A|$ に対する スケーラビリティ である. 物流倉庫の例に話を戻すと, 小規模でも十数台, 大規模だと数千台のロボットを動かす需要があるので, 理想的なアルゴリズムはその規模に耐えてほしい. そして A* を直接適応する方法はまったくスケーラブルではなく, せいぜい $|A| \approx 10$ 程度で限界であり, 現実的な時間で解を得ることがまったくできなくなる.

A* がなぜスケーラブルでないかというと, 結果として出来上がるグラフ $H$ が超巨大になるためである. もう少し正確に記述すると, ある構成 $Q$ から遷移可能な構成の数は $O \left((\Delta + 1)^{|A|} \right)$ と述べた. グリッドを想定して $\Delta + 1 = 5$ とし, $|A|$ に対して具体的な値を計算してみると,

• $5^5 = 3,125$
• $5^{10} = 9,765,625$
• $5^{20} = 95,367,431,640,625$

という感じで, すごい数字になることがわかる. つまり, エージェントのチームのサイズが大きくなるにつれ, 遷移可能な構成を列挙することが絶望的になるのである. この遷移可能な構成の数のことを branching factor と呼ぶが, MAPF 自体を一つの経路計画と見做すと, branching factor が大きすぎて素朴な A* は使い物にならない.

この問題を解消すべく, A*を MAPF 用に魔改造したアルゴリズムが提案されている [Standley AAAI-10] [Goldenberg+ JAIR-14] [Wagner+ AIJ-15]. 特に [Standley AAAI-10] は 今日の MAPF 研究の火付け役となった論文である. それでも, この方向性ではスケーラビリティに難があるのが現状だ.

二段階の探索: CBS

さて, MAPF を巨大なグラフの経路探索として表現すると手に負えないことが分かった. MAPF を実用的にするには, 異なる表現方法をもつ必要がある. そこで Conflict-Based Search (CBS) [Sharon+ AIJ-15] というアルゴリズムを紹介する.

CBS は 低レベルの探索 と呼ばれるシングルエージェントの経路計画と, 高レベルの探索 と呼ばれる経路同士の衝突管理を行う, 二つの探索アルゴリズムから構成される. 大雑把に言うと, CBS はこの二つを交互に実行することで衝突のない経路を見つける. 具体的には,

• 高レベルの探索は, 低レベルの探索によって得られた経路の組合わせに衝突があるかを判断する. 衝突がない場合, それが解になる. 衝突がある場合, 低レベルの探索に経路をリクエストする. このとき, 見つかった衝突を避けるように制約を課す.
• 低レベルの探索は高レベルの探索が課す制約に従いながら経路を探し, 解候補を作る. これは A* などで実行可能だ.

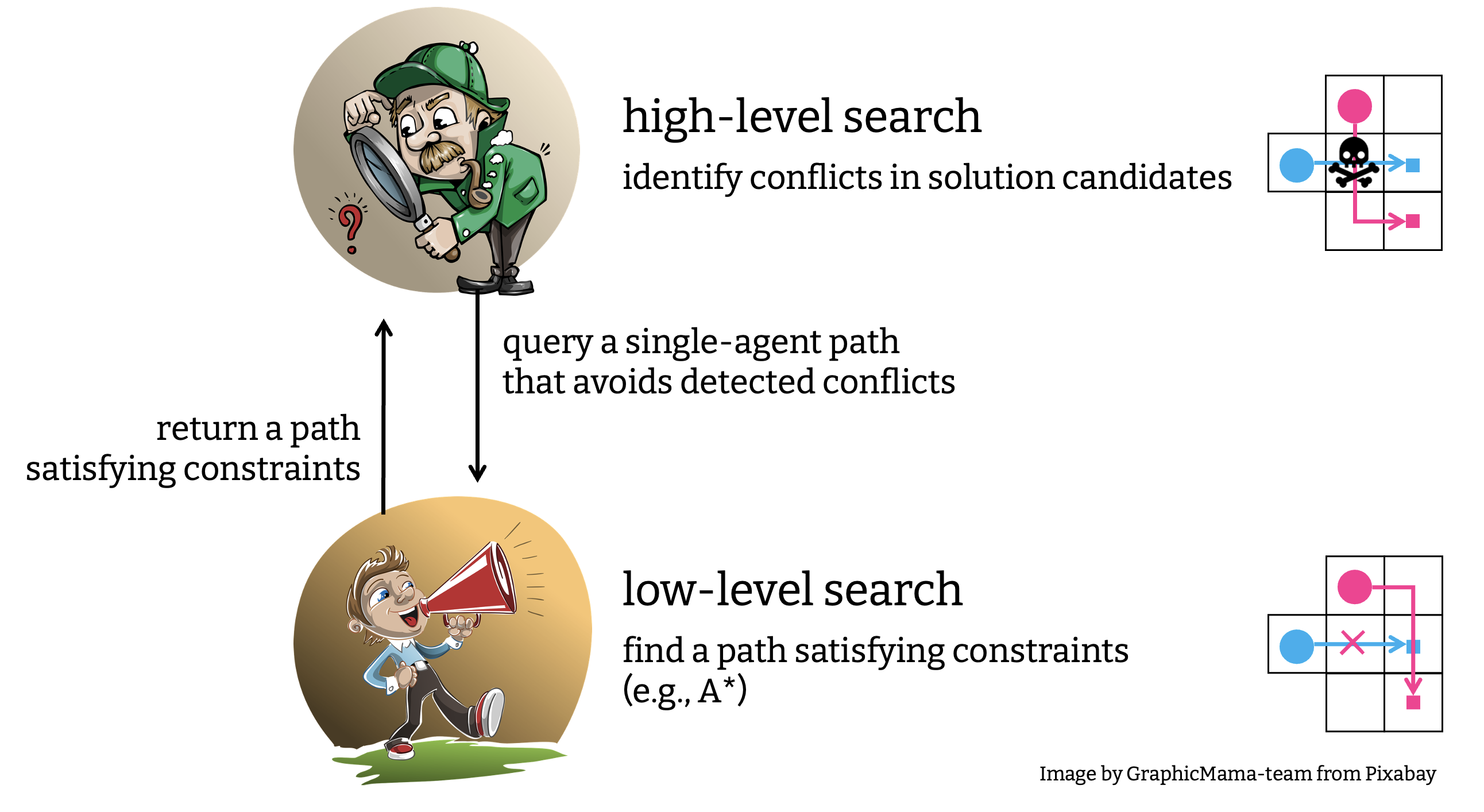
CBS の低レベルの探索は単なるシングルエージェントの経路計画だが, 高レベルの探索は少し独特なので詳細を加える.

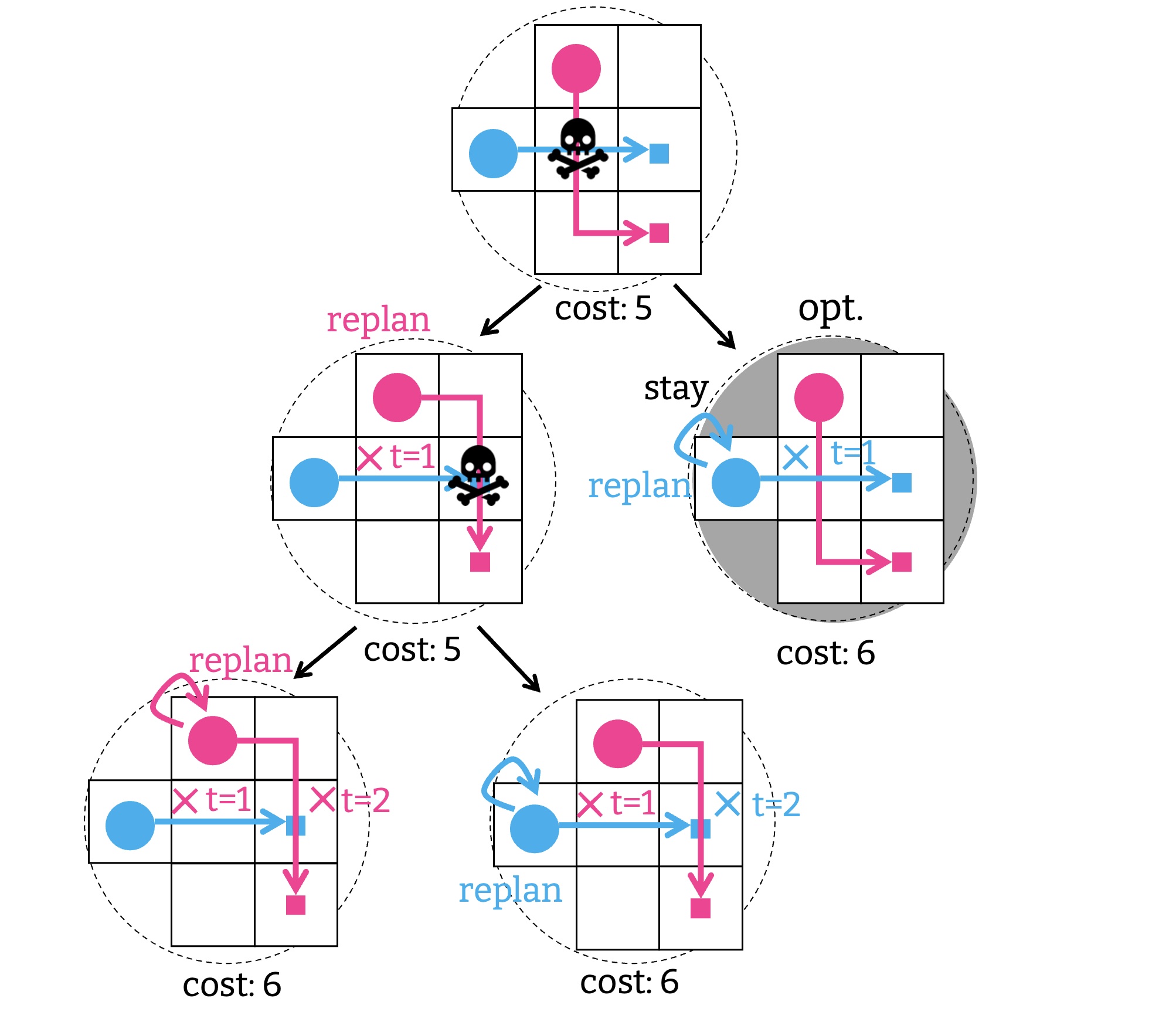
まず, 衝突を無視して最短経路を計算した, 下図の経路の組合わせを見てみる. これには 時刻 $1$ で真ん中の頂点 $v \in V$ に衝突がある. なのでこれは実行可能解ではない.

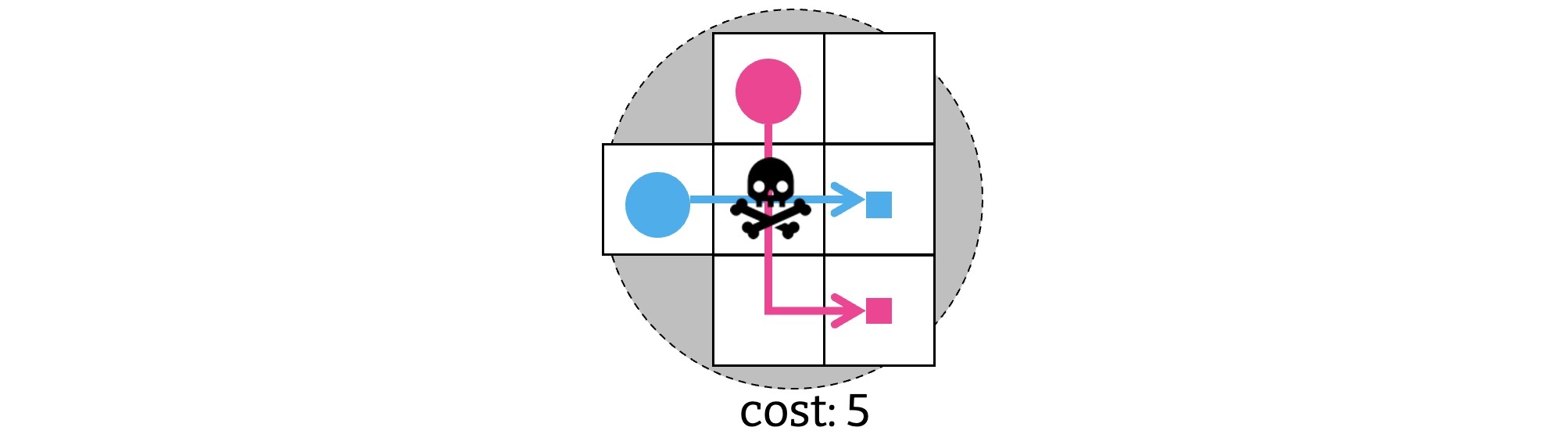
この衝突を防ぐ方法として, 次の二つのパターンを考えることができる.

• 赤いエージェント $r$ の時刻 1 での頂点 $v$ の使用を禁止する. 以下, これを $\langle 1, v, r \rangle$ の制約を課す, と呼ぶことにしよう.
• 青いエージェント $b$ に対しても同様に, 時刻 $1$ での $v$ の使用を禁止する. つまり $\langle 1, v, b \rangle$ を課す.

この考えに則り, オリジナルの経路の組合せ, つまり解の候補から新しい解の候補を二つ作る. 具体的には:

• 低レベルの探索を使って, $\langle 1, v, r \rangle $ を満たす赤いエージェントの経路を再計画する. 青いエージェントの経路をそのまま使って, 解の候補を一つ作る. (左の子)
• 青いエージェントに対しても $\langle 1, v, b \rangle$ を満たす経路を計算し, 解の候補を作る. (右の子)

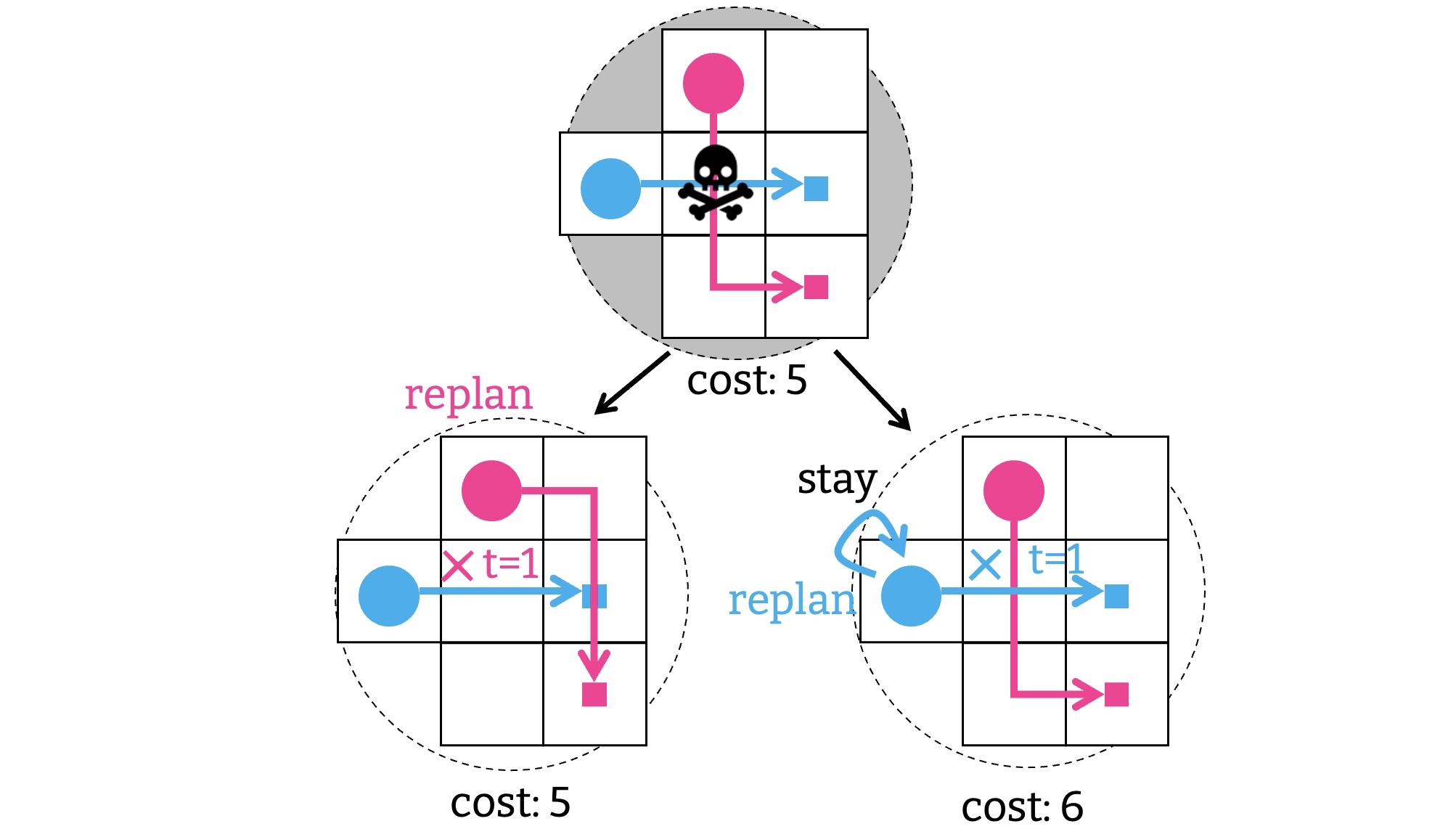
次に, 新しく作られた解候補に衝突があるか見てみよう. まず, 制約 $\langle 1, v, r\rangle$ に従って, 赤いエージェントの経路を再計画した場合について確認する (左の子). これには時刻 $2$, 頂点 $u$ で新しい衝突が含まれている. したがって, 新しい制約 $\langle 2, u, r\rangle$ と $\langle 2, u, b\rangle$ を考えて, それぞれに対して解の候補を作り直す. このとき, オリジナルの制約 $\langle 1, v, r \rangle$ を引き継ぐことに注意されたい. つまり, 片方は制約のリスト $[\langle 1, v, r \rangle, \langle 2, u, r\rangle]$ をすべて満たす必要があり, もう片方は $[\langle 1, v, r \rangle, \langle 2, u, b\rangle]$ を満たす必要がある.

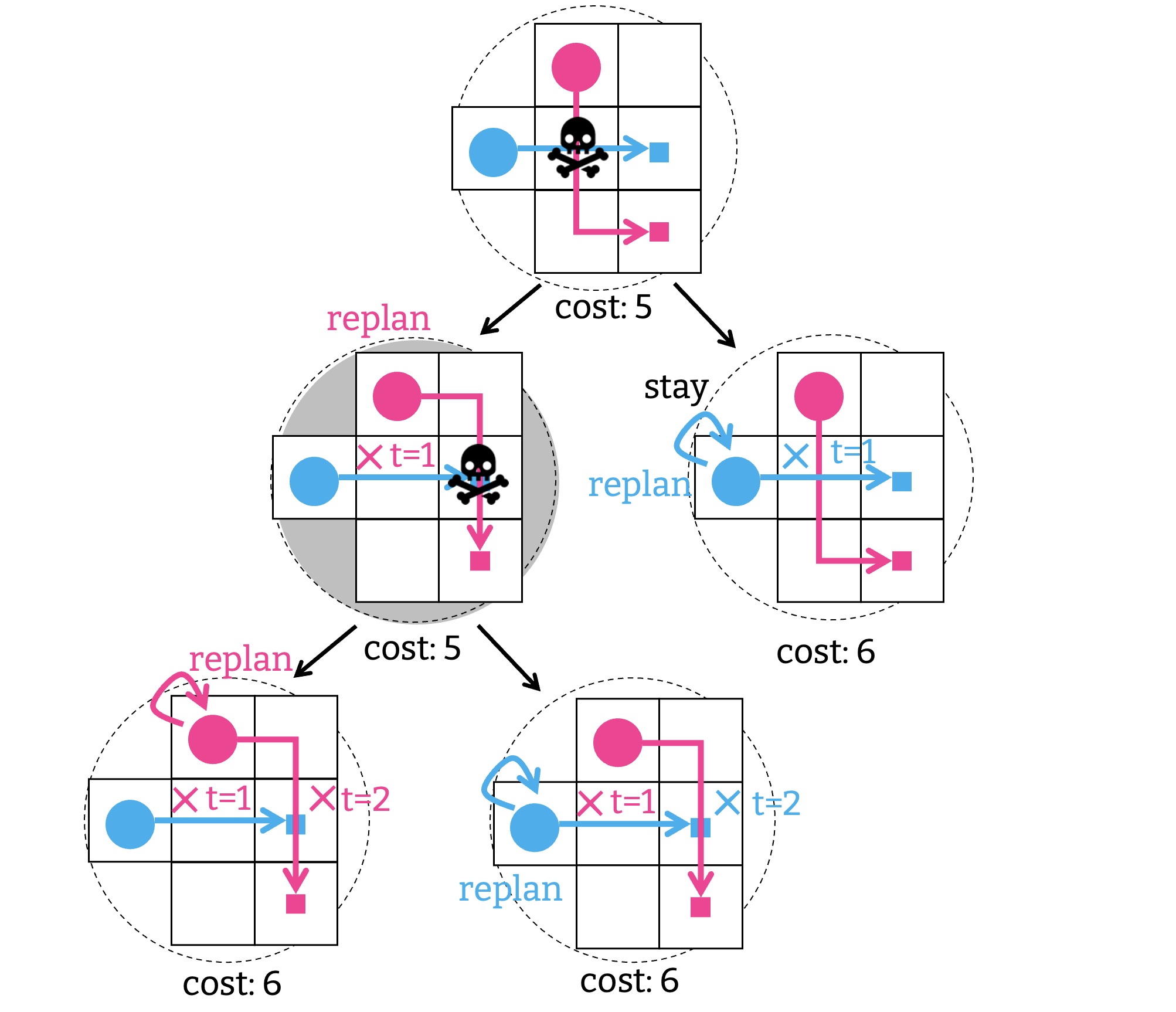
CBS は同様の処理, つまり制約を足して解の候補を作るプロセスを, 衝突がない解候補が見つかるまで繰り返す. 例えば, 最初の解候補に制約 $\langle 1, v, b \rangle$ を課した場合 (右の子), 衝突はないので, これが解になる.

さて, 衝突管理を行う高レベルの探索を見てきたが, これも経路計画とみなすことができる. 解候補を生成するときに課される制約の集合をグラフの頂点とみなそう. このグラフにおいて, ある頂点 $N$ から遷移可能な頂点とは, $N$ に制約を一つ加えたものが該当する. 例えば, 最初の解候補に課される制約はなにもないので $\emptyset$, これが開始頂点だ. 上のイラストに倣って開始頂点に制約 $\langle 1, v, r \rangle$ か $\langle 1, v, b \rangle$ を加えると, 二つの頂点 $[\langle 1, v, r \rangle]$, $[\langle 1, v, b \rangle]$ を作ることができる. $[\langle 1, v, r \rangle]$ からはさらに $[\langle 1, v, r \rangle, \langle 2, u, r\rangle]$ と $[\langle 1, v, r \rangle, \langle 2, u, b\rangle]$ を作ったのだった. こんな具合にすると, 衝突管理を行うグラフを作ることができる. CBS の高レベルの探索は, このグラフ上で解が見つかるまで A* を走らせているようなものだと理解できる.

ここで, CBS は全部の可能性を列挙しないという点に注目してほしい. 例えば, 開始頂点に時刻 5 に対する制約 $\langle 5, v, r \rangle$ を加えることもできるが, まったくもって意味がない. 代わりに CBS は衝突管理に必要最小限のグラフを作る. これによって効率的に解を見つけることができるカラクリだ.

実際, CBS は素朴に A* を MAPF に適用するよりも遥かにスケーラブルである. また, 綺麗な構造をしていることもあり, たくさんのパワフルな拡張が提案されてきた [Boyarski+ IJCAI-15] [Felner+ ICAPS-18] [Gange+ ICAPS-19] [Li+ ICAPS-19] [Li+ AIJ-21] [Zhang+ AIJ-22]. また, CBS のように徐々に制約を課していくという構造は還元ベースのアプローチにも取り入れられている [Surynek IJCAI-19] [Lam+ COR-22]. これは, MAPF を整数計画問題や SAT など他のよく知られた問題に還元して解を得る方法である.

今日, CBS は最も人気なアルゴリズムであるが, 十分にスケーラブルかと言われると, そうではない. 種々様々な拡張を導入して, 実装を最適化して, ようやく百台程度のエージェントのチームを捌くことが見えてくる. それ以上は現状だと難しい.

最適性を犠牲にする: 有界準最適性なアルゴリズム

ここまで A* の適用と CBS という二つのアルゴリズムを見てきた. そしてどちらも巨大なグラフ (通常, 探索空間と呼ぶ) に対して経路計画 (探索) を実行するものであると説明した. 多くの場合, 経路計画はグラフ上の最短経路を求めることに興味があるが, MAPF は馬鹿みたいに巨大な問題なので, 最短経路は現実的な時間で求まらないことが多い. となると, 解がまったく得られないよりは, 多少のクオリティは犠牲にしたとしても, 解が時間内に得られる方が遥かに良い.

問題はどこまでの犠牲を許容するかだ. これに対して, 最適解からのギャップを任意に調整することができる便利なアルゴリズムのクラスが存在する. 具体的に, あるパラメータ $w \in \mathbb{R}_{\geq 1}$ が与えられたとき, アルゴリズムが出力する解のコストを $c$ とする. 最適解のコストを $c^\ast$ として, 常に $c \leq wc^\ast$ を満たすことが保証されるとき, そのアルゴリズムを有界準最適であると呼ぶ.

A* のような構造が存在するのであれば, 有界準最適バージョンを作るのは比較的簡単だ. 例えば, A* は各イテレーションで $f(N) := g(N) + h(N)$ が最小となる探索ノード $N$ を処理する. ここで $g(N)$ は $N$ に到達するまでのコスト, $h(N)$ はゴールに到達するまでの見積もりコストで, ヒューリスティックと呼ばれる. $f$ の代わりに $f_w(N) := g(N) + w h(N)$ を使うと, Weighted A* と呼ばれるアルゴリズムになる. $h(N)$ の見積もりが本当のコストよりも常に小さいのであれば, つまり許容可能である場合, Weighted A* は $c \leq wc^\ast$ を満たす解を返す [Pearl 84].

同様の試みは A* の MAPF 版や CBS といったアルゴリズムに対しても適用可能で, 有界準最適な MAPF アルゴリズムが存在する [Wagner+ AIJ-15] [Barer+ SoCS-14] [Li+ AAAI-21a]. これらのアルゴリズムは解のクオリティを保証しつつ, オリジナルのアルゴリズムのスケーラビリティを改善している.

素朴な方法: PP

解の最適性を犠牲にすることで, スケーラビリティは改善されるが, リアルタイムに MAPF を解くフィードバックを回せるかというと, それでもかなり難しい. そこで, 理論的な保証は弱いが, 使い勝手の良い PP (Prioritized Planning) [Erdmann+ 87] [Silver AIIDE-05] という方法を見てみよう.

PP は次の二つのステップで実行できる.

1. 各エージェントに優先順位を何らかの方法で割当てる.
2. 優先順位に従って, 各エージェントの経路を 順番に 計画する. ただし, 先に計算された経路と衝突がないようにする.

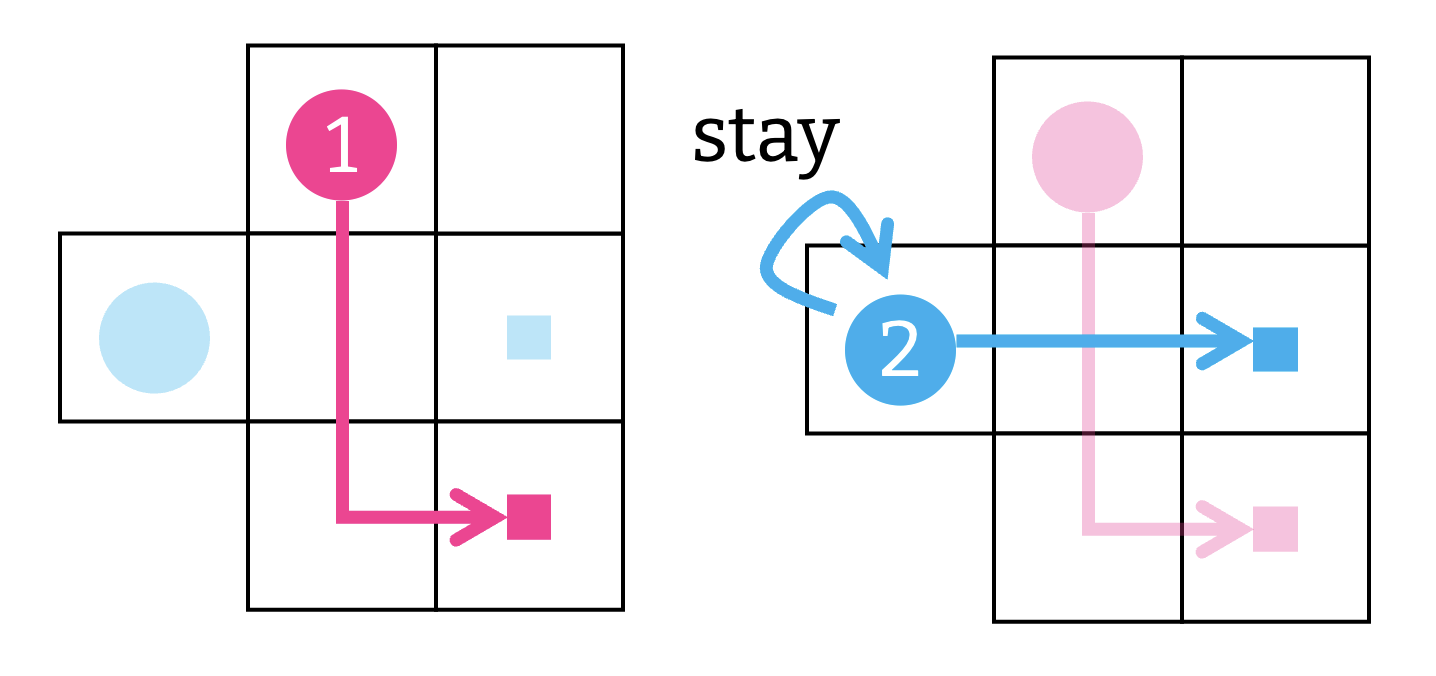
随分シンプルな手続きだが, これまで見てきたアプローチよりもスケーラブルで, そこそこ良い解を返すし, 何より実行しやすい. MAPF を解きたければ, 最初に試すのは PP が良いだろう.

PP もよく研究されていて, 例えばステップ 1 でどのように優先順位を与えるのが良いかの指針は複数あるし [Bennewitz+ Robot. Auton. Syst.-02] [van den Berg+ IROS-05] [Wu+ ICRA-20], ステップ 2 を少し捻って特定の状況に限定すると, 必ず実行可能解を見つけることができる [Čáp+ T-ASE-15].

じゃあこれでいいじゃないか, というと, そうでもない. PP はスケーラブルであると言ったが, 少し正確性を欠いた. より正確には, PP は複数エージェントを “共同して” 動かす必要がないインスタンスに対してはスケーラブルである. 例えば下図のように, 青, もしくは赤いエージェントをいったん脇に避ける必要がある問題を PP は解くことができない. たった二台であるにも関わらずだ. 一方, “スケーラブル” でない A* の適用や CBS といった網羅探索を行うアプローチでは, このような問題は難なく解決できる.

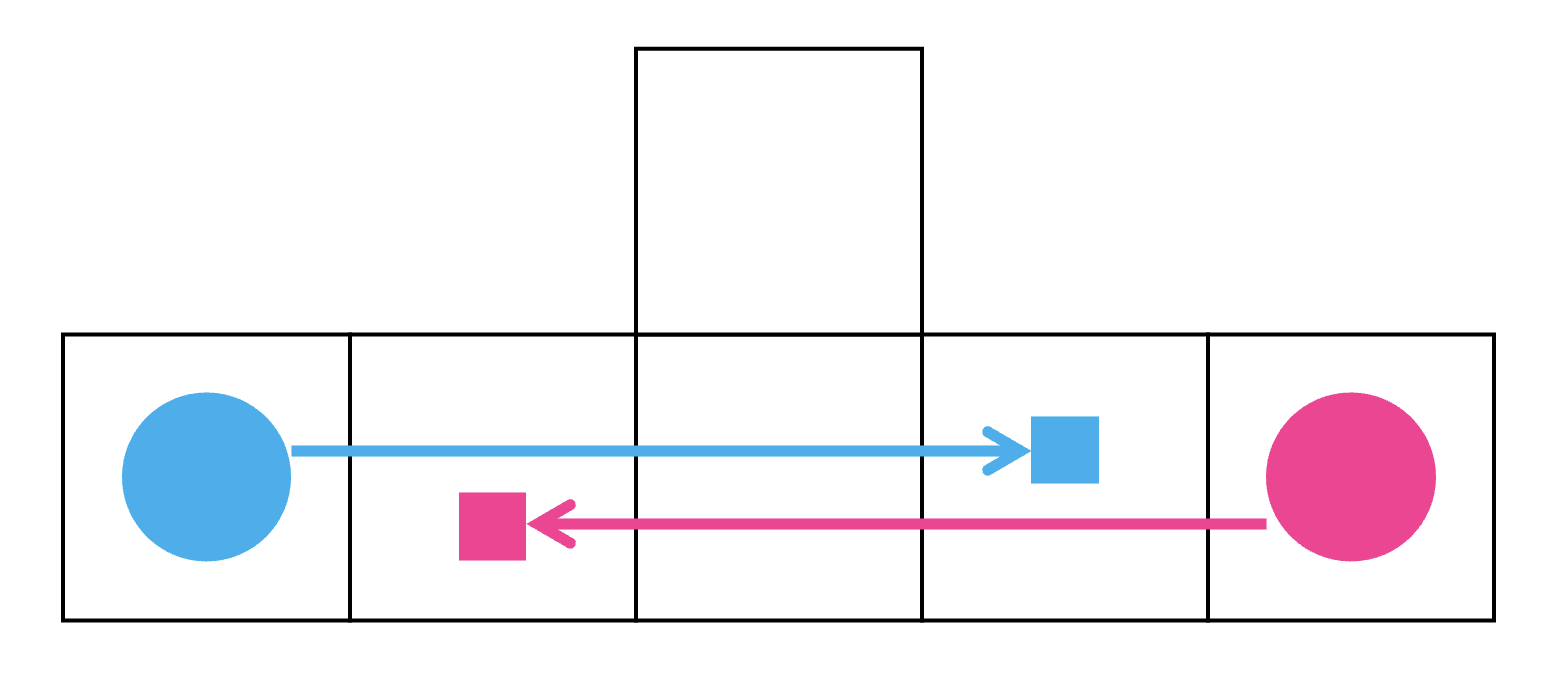
都合の悪いことに, 実環境では敵対的な状況に遭遇することがよくある. とはいえ, PP はこれまでに紹介したアルゴリズムよりも多くのエージェントを扱うことができ, この点は魅力的だ. この方向に沿って, 解を見つける保証がない, より “スケーラブル” なアルゴリズムを見ていこう.

メタアルゴリズムその1: LNS2

次に見るアルゴリズム LNS2 (Large Neighborhood Search) [Li+ AAAI-22] は, 他の MAPF アルゴリズムをサブルーチンとして使用する メタアルゴリズム である. LNS2 は CBS のように二段階の構造をもっている. 具体的には, 次のプロセスを衝突がない経路の組合せが見つかるまで繰り返す.

1. 衝突を含んだ経路の組合せ (解の候補) に対して, エージェントのチーム $A$ のサブセット $B \subseteq A$ を決める.
2. $B$ に含まれるエージェントの経路を, $A \setminus B$ の経路と衝突を避けながら再計画する. このとき $B$ の経路の組合せに含まれる衝突の数をなるべく抑える.
3. もともとの解候補における $B$ の経路を, ステップ 2 で得られた経路に置き換えて, 解候補を更新してステップ 1 に戻る.

肝となるのがステップ 2 で, これには CBS の派生や PP などを適応して使うことができる. ステップ 1 における効果的なサブセット $B \subseteq A$ の特定は, LNS2 のパフォーマンスが他アルゴリズムに依存することもあり, 正直よく分かっていない.

もちろん LNS2 には理論的な保証は何もない. 特に, PP が失敗する敵対的なインスタンスでは LNS2 も同じように失敗することがある. ただシンプルで実行しやすく, 何よりも “スケーラビリティ” が素晴らしい. コンセプト的にも実証的にも, LNS2 は単に PP を走らせるより強力であり, 現在 PP を単独で使うメリットはほぼない.

極端にスケーラブルな方法: PIBT

LNS2 の “スケーラビリティ” には目を見張るものがあるが, 千台規模のチームに対してリアルタイム, 例えば十秒以内に MAPF を解き続けられるかというと, かなり厳しい. そのような状況には PIBT (Priority Inheritance with Backtracking) [Okumura+ AIJ-22] という軽量なアルゴリズムが適している. PIBT は 万単位のエージェント群の動作生成も可能だ.

このアルゴリズムは今まで紹介してきたものと違って, MAPF を解くこと “も” できるアルゴリズムだ. A* の適用のパートですべてのエージェントの位置を構成と呼び, $Q \in V^{|A|}$ で表したが, PIBT は構成から遷移可能な別の構成を生成するアルゴリズムである. より正確には,

• 構成 $Q^{\text{from}}$
• 各エージェントがどの行動をとりたいかについての嗜好
• 各エージェントの優先順位

の三つを入力にとって, $Q^{\text{from}}$ から遷移可能な別の構成 $Q^{\text{to}}$ を生成する. 新しい構成 $Q^{\text{to}}$ はエージェントの嗜好と優先順位を可能な限り反映しながら作られる.

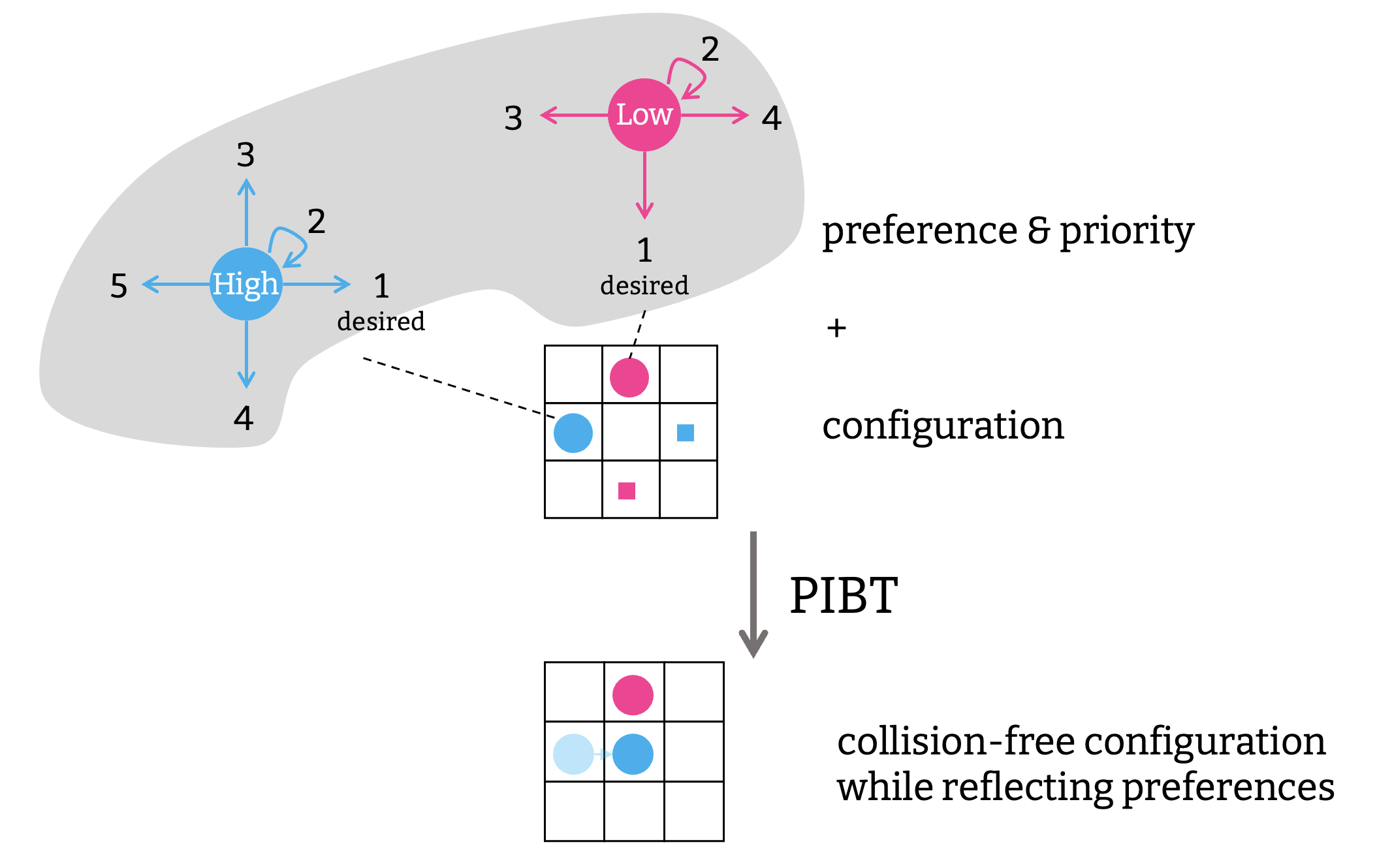
PIBT を使うと, MAPF のスタートの構成 $Q_0 = \mathcal{S}$ から時刻 1 の構成 $Q_1$ を作り, $Q_1$ から $Q_2$ を作り…, といった塩梅で連続的に構成を生成することができる. 仮にゴールとなる構成 $\mathcal{T}$ に到達すると, 衝突のない経路の組合せが出来上がる. なので PIBT は MAPF “も” 解くことができるというわけだ. MAPF に適用するにあたり, エージェント $i \in A$ の嗜好は $i$ が行動した結果の地点からゴール $g_i \in V$ までの距離でソートすればよく, 優先順位も同様にゴール $g_i$ までの距離で作ることができる. もちろん, このアルゴリズムは必ず解を見つけることを保証しない.

肝心のどうやって構成を生成するかについては, 再帰を使ってスッキリと書き下すことができる. 簡単なので, 下に [Okumura IJCAI-23] から引っ張ってきた疑似アルゴリズムを掲載しておこう.

大雑把に言えば, 疑似アルゴリズムは次のステップを実行している.

• 優先順位 (L1: $A$ がソートされていると考えてほしい) と嗜好 (L5: $C \subseteq V$) に従って, エージェント $i \in A$ に次の場所 $v \in C$ を割当てていく (L8).
• このときエージェント $i$ と, まだ場所が割当てられていない他のエージェント $j \in A$ との間に衝突が発生しそうであれば (L10), 優先順位を無視して, $j$ に場所を割当てようとする. これが再帰に該当する.
• $j$ の割当てが失敗したら $i$ は場所 $v$ を諦めて, 嗜好 $C$ に従って次の場所を獲得しようとする.

疑似アルゴリズムから想像できるように, PIBT はとても軽量で, 2024年現在, 最も “スケーラブル” な MAPF アルゴリズムの一つである. あくまでグリーディーに構成を生成するため, 得られる解のクオリティはそこまでよくない. ただ, 最近の研究によると [Chen+ AAAI-24] [Zhang+ arXiv-24], 嗜好の作り方を工夫することで, スピードを維持したまま探索ベースの方法に匹敵する解を作ることができるらしい.

メタアルゴリズムその2: LaCAM

最後に, 近年の MAPF 研究で最も衝撃的な方法を紹介しよう. LaCAM (Lazy Constraints Addition Search) [Okumura AAAI-23] である. ²

LaCAM は LNS2 と同様, 他の MAPF アルゴリズム $\mathcal{M}$ をサブルーチンとして使用するメタアルゴリズムであり, $\mathcal{M}$ のパフォーマンスを引き継ぎながら網羅探索を行う. 実は LNS2 は任意のアルゴリズムを使うことはできないのだが, LaCAM はこの規制が緩く, [Li+ AAAI-21b] などのテクニックと組合せると, ほぼすべての MAPF アルゴリズムを使えてしまう. その中でも PIBT との組合せは強力で, 一万台規模のエージェント群を扱いつつ, PP が陥るようなエッジケースも解決する, 真にスケーラブルな方法を実現できる.

ではアルゴリズムを見ていこう. ベースとなるのは A* の MAPF への適用である. A* の課題は, ある構成から遷移可能な構成の数が膨大で, それら すべてを同時に 列挙することが実質的に不可能な点にあった. LaCAM はこの作業を先延ばしにして, ゴールに到達しやすそうな “有望な” 構成から 一つずつ 調べていく. その際, 有望な構成を決めるのに他の MAPF アルゴリズム $\mathcal{M}$ を利用する. この方法を使うと, $\mathcal{M}$ が良き道案内として機能するかぎり, ゴールの構成を見つけるまでに生成される構成の数を劇的に減らすことができ, 高速な MAPF を実現する.

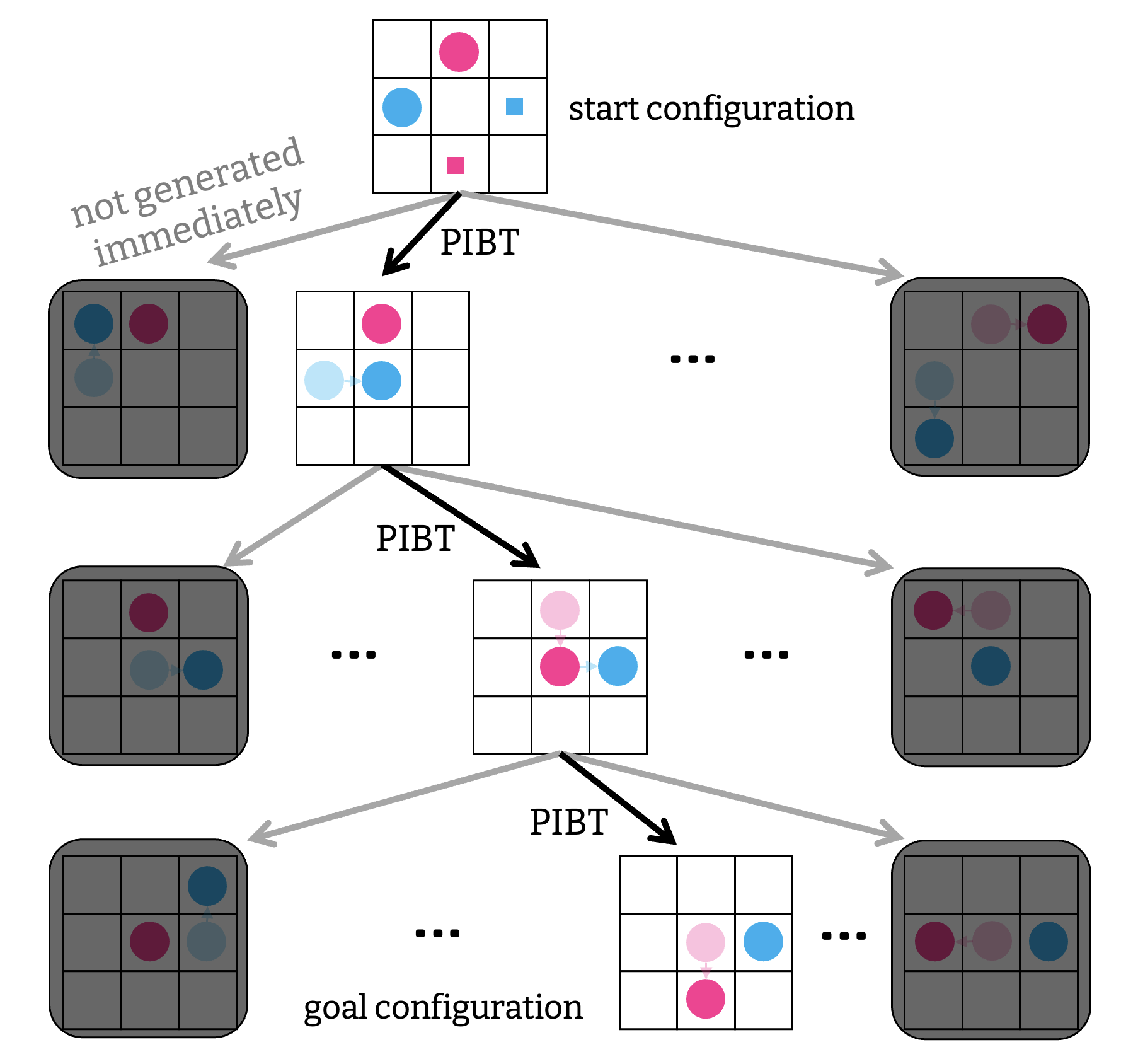
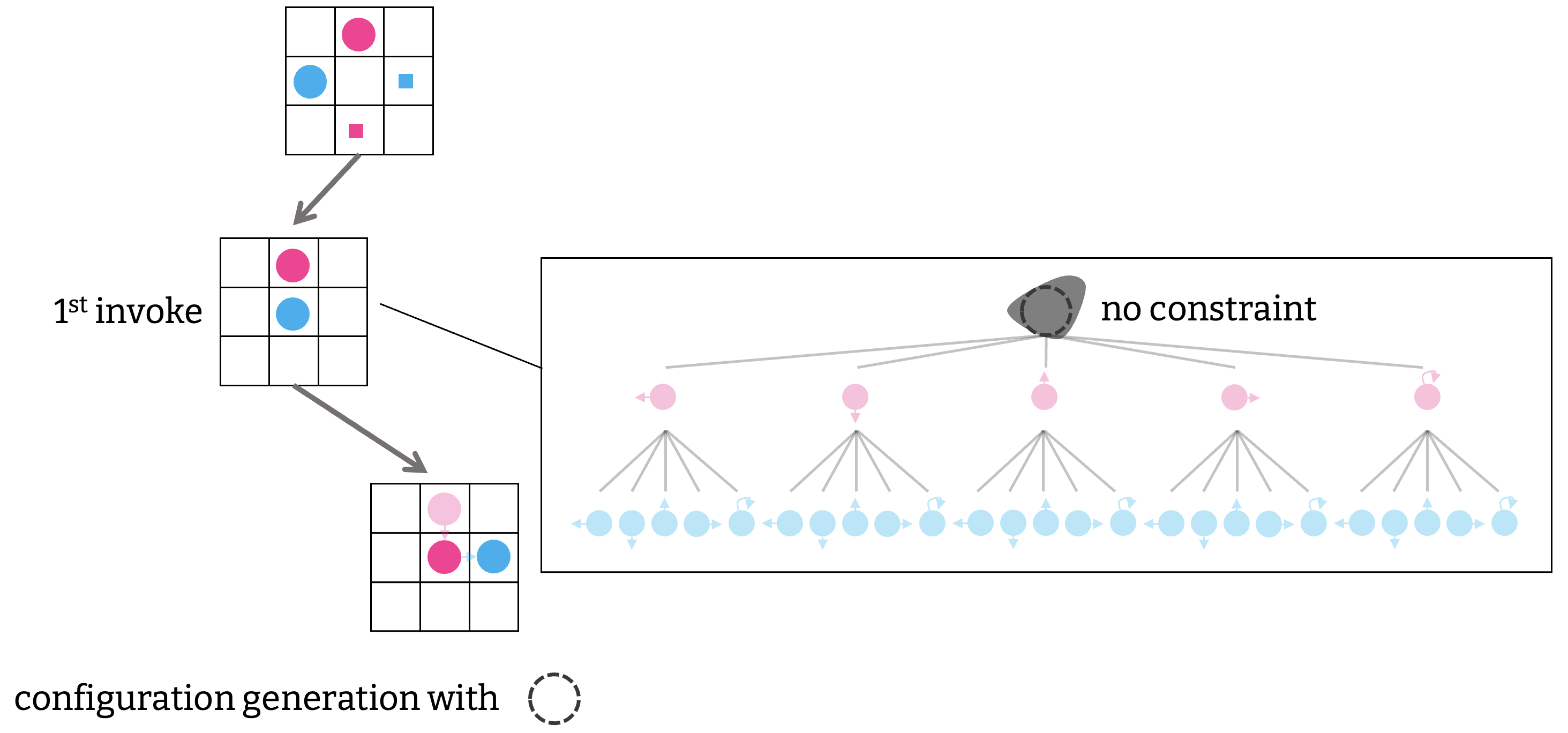
ただ, 最終的には, ある構成 $Q$ から遷移可能な構成をすべて調べる必要があり, 構成の遅延生成をどうやってか実現する必要がある. これは CBS と似たような塩梅で, 構成の生成に制約を徐々に足していけばいい. 例えば, 最初の構成生成では何も制約を課さないが,

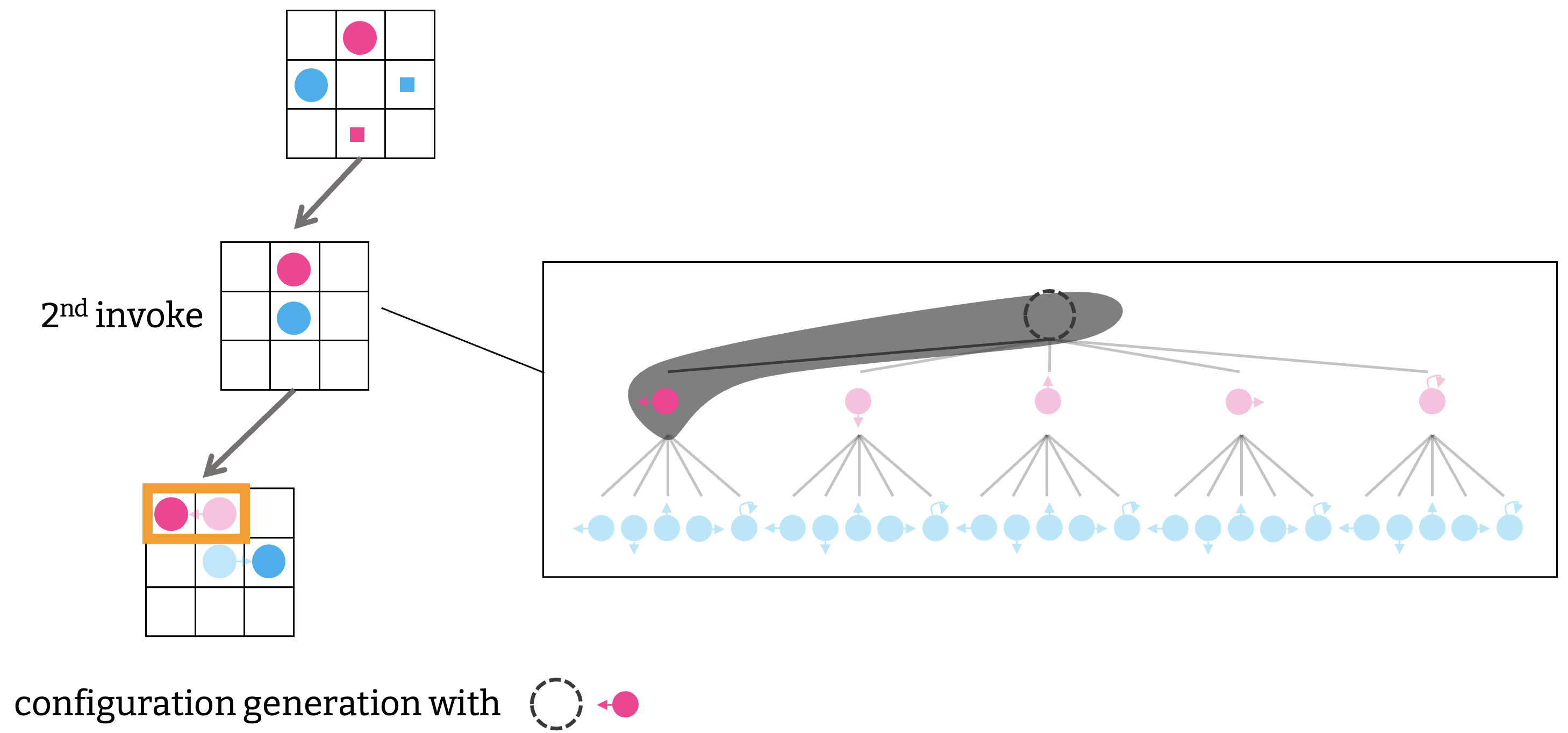
二回目の生成では, 「赤いエージェントが左に移動する」という制約を加える.

同様にして, 構成を生成する度に制約を追加していく. このプロセスは「どのエージェントが次, どこに行くか」かについての探索, 例えば幅優先探索を行うことで実現される.

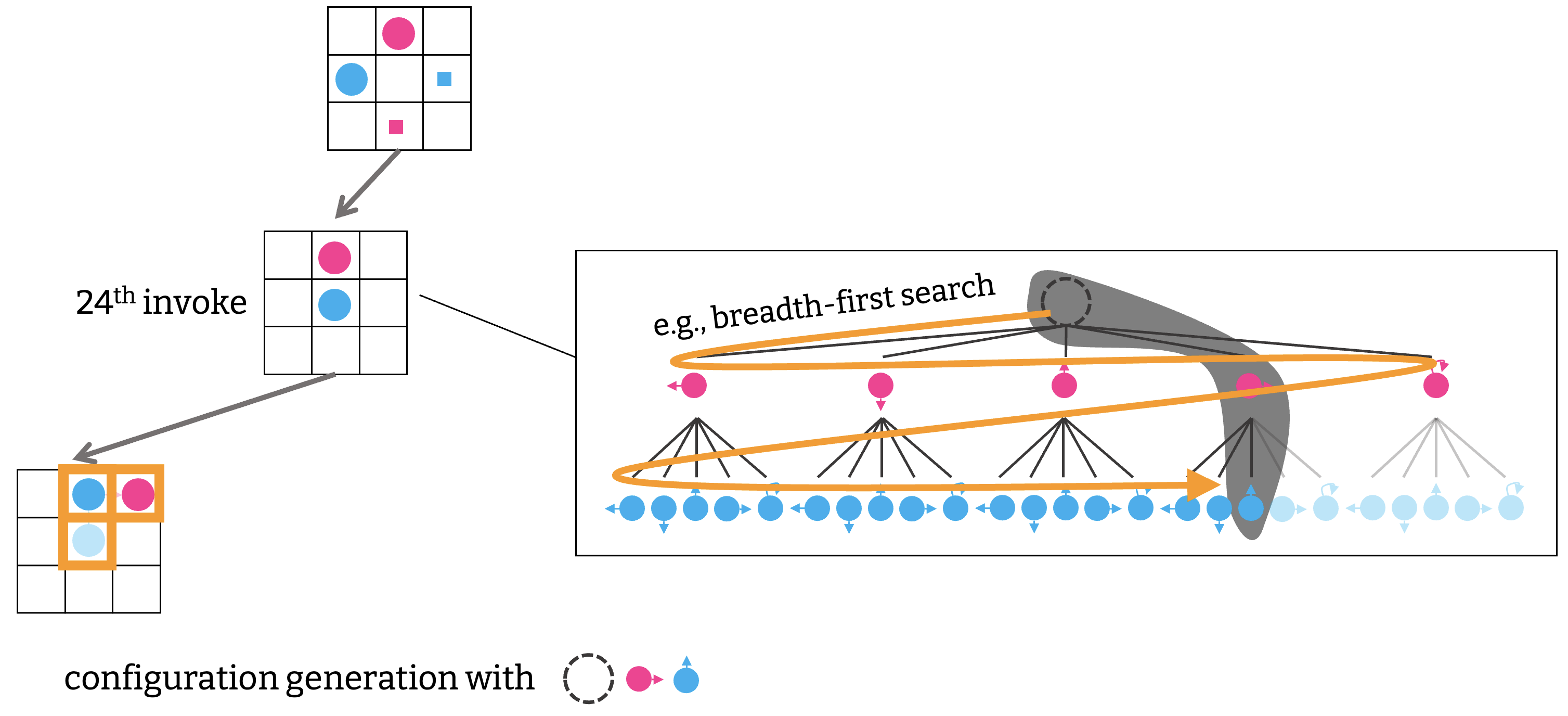
つまり LaCAM も CBS と同様, 二段階の探索から構成される. ただし役割が逆転していて, CBS は高レベルの探索が制約を課すのに対し, LaCAM は低レベルの探索で課された制約に従って, 高レベルの探索が進む.

オリジナルの LaCAM は得られる解のコストに対して保証がなかったが, LaCAM* という, いつか最適解に収束するアルゴリズムが提案されている [Okumura IJCAI-23]. また, LaCAM はメタアルゴリズムなので, サブルーチンで使用するアルゴリズムを改良すると, LaCAM 自体のパフォーマンスも向上する [Chen+ AAAI-24]. その他パフォーマンスを向上させるテクニックは色々あり [Okumura AAMAS-24], 他の MAPF アルゴリズムでは難しいとても混雑した問題でも, 短時間でかなり良い解を得られるようになっている.

もともとの LaCAM (左) vs. 最近の LaCAM (右)

アルゴリズムのまとめ

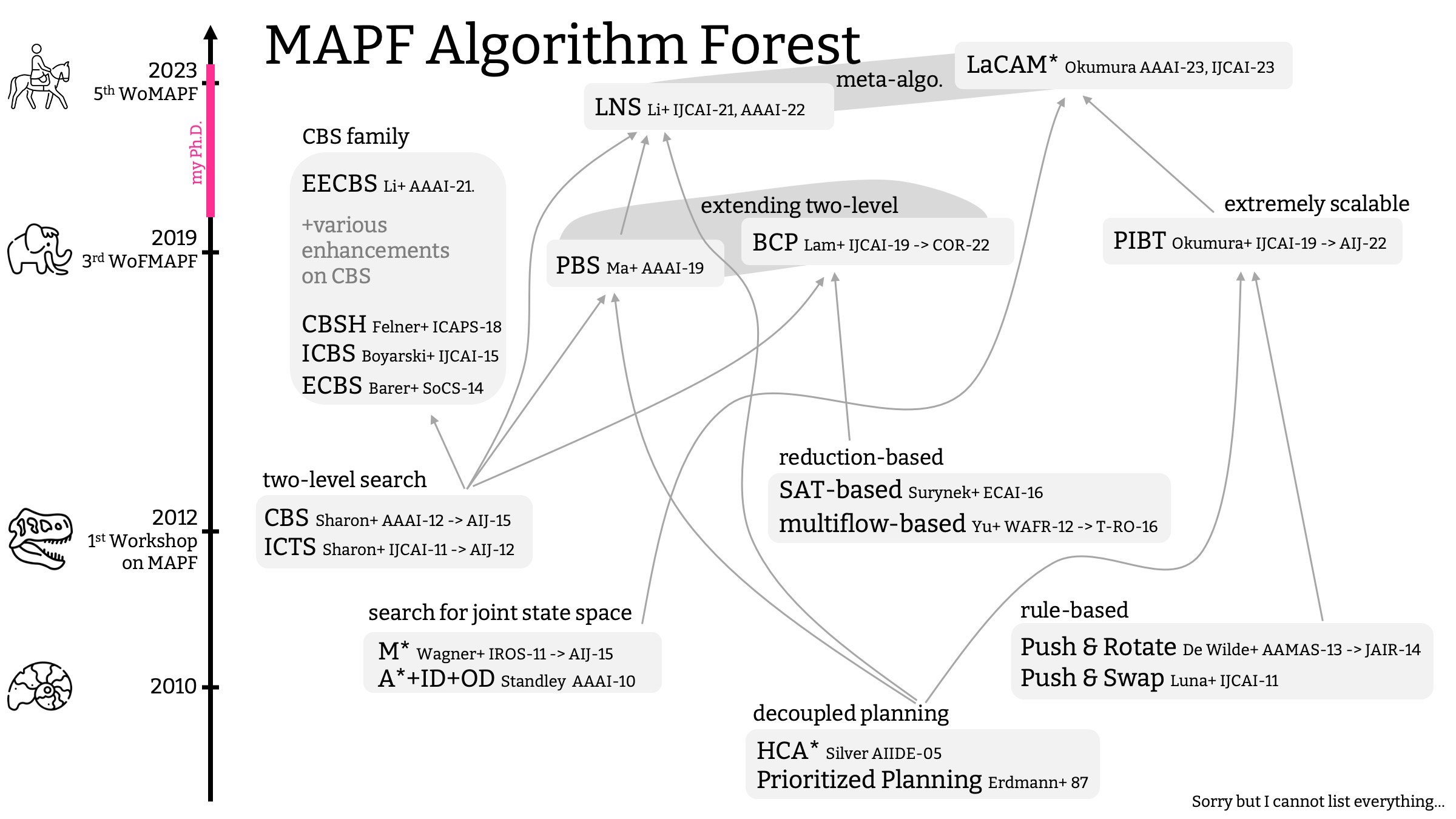
以上でアルゴリズムの紹介を終えるが, MAPF は汎用的で応用性の高い技術のため, 様々なアプローチが開発されてきたし, また開発され続けている . 例えば, 説明をスキップしたものだと,

• CBS と同時期に誕生した二段階の探索である ICTS (Increasing Cost Tree Search) [Sharon+ AIJ-13]
• MAPF を SAT [Surynek+ ECAI-16] やマルチフロー問題 [Yu+ T-RO-16] など, 他のよく知られた問題に還元するアプローチ
• CBS と PP を組合せた PBC (Priority-Based Search) [Ma+ AAAI-19]
• 数理最適化の技術を適用した BCP (Branch-and-cut-and-price) [Lam+ COR-22]
• ルールベースの多項式アルゴリズムである Push & Swap/Rotate [Luna+ IJCAI-12] [de Wilde+ JAIR-14]
• 模倣学習や強化学習を使ってエージェントごとのポリシーを学習するアプローチ [Sartoretti+ RA-L-19] [Li+ IROS-20]

などがある. 下に主要な MAPF アルゴリズムと, 各アルゴリズムがどのように先行研究に影響を受けているか, タイムラインに沿ってまとめた図を用意した.

これだけたくさん方法があると, 結局どのアルゴリズムを使えばいいのという質問がでてきそうなので, 指針を載せておこう.

• 最適解や解コストに保証がほしいなら CBS ベース.
• とりあえず試したいのであれば PP. その後, パフォーマンスを上げたかったら PBS / LNS2 あたりを試す.
• 大規模な問題を高速に解きたかったら PIBT / LaCAM .
• 準最適解の逐次改善は可能である [Okumura+ IROS-21] [Li+ IJCAI-21].

派生問題

MAPF は基礎的な問題なため, 実際のアプリケーションにもっていくには一捻りする必要がある. とはいえ, そういった問題の多くは, これまで見てきたアルゴリズムを適用して解くことができる. ここでは MAPF の派生問題を眺めてみることにする.

終わりがない MAPF とタスク割当て

素朴な MAPF から離れて, もう少し実践的な環境を想定したときに,

• 継続的に MAPF を解き続ける必要性, つまりエージェントがゴールに到達しても終わらない MAPF システムと,
• タスク割当て, つまりどのエージェントをどこに向かわせるかを決めること

の二点を取り入れることが多い. 前者の代表格は Lifelong MAPF [Li+ AAAI-21b] と呼ばれるもので, これはエージェントがゴールに到達したら即座に新しいゴールがアサインされ, 永遠と MAPF を解く必要がある設定である. 実行中にエージェントが増えたり減ったりする設定である Online MAPF [Švancara+ AAAI-19] も, 継続して MAPF を解く必要がある設定である. 後者の代表格は, タスク割当てと経路計画を同時に解く TAPF (Combined Target Assignment and Pathfinding) [Ma+ AAMAS-16] [Honig+ AAMAS-18] という問題で, CBS を利用したアルゴリズムがいくつか存在する. TAPF の極限は任意の目的地を任意のエージェントに割当てることができる設定で, Anonymous MAPF もしくは Unlabeled MAPF と呼ばれている. これは ロボット群のパターン形成などに使うことができ, ここまで紹介してきたアルゴリズムを充てることもできるが, それよりも計算が安価なアプローチが存在する [Yu+ WAFR-13] [Okumura+ AIJ-23] [Ali+ AAAI-24]. 継続的に MAPF を解く必要性とタスク割当ての二つを取入れた MAPD (Multi-Agent Pickup and Delivery) [Ma+ AAMAS-17] という問題も存在していて, これは自動倉庫の荷物搬送を模している. MAPD は CBS, PP, PIBT などを適用して解くことができる.

移動時間に関する不確実性

最終的には, MAPF で得られた解を, 実際のシステムで使うことに興味がある. だいたいの応用先は移動ロボットだが, 実際のロボットを動かす場合, MAPF が指定した時刻通りに動いてくれるかというと, まったくそんなことはない. トラッキングのパフォーマンスを上げるのは大事だが, もう一つの方向性は, 初めから実システムの不確実性を考慮してプランニングすることだ. 例えば Robust MAPF [Atzmon+ JAIR-20] は, エージェントがある程度は遅延したとしても衝突がない経路を見つけることを目的としている. 同様に, エージェントの移動時間をモデリングして, 安全な経路を見つける研究としては [Wagner+ ICAPS-17] [Shahar+ JAIR-21] などがある. この方向と対象的なのが OTIMAPP (Offline Time-Independent Multiagent Path Planning) [Okumura+ T-RO-23] という問題で, 衝突回避をエージェントに任せて, 代わりにエージェントがどのタイミングで動いてもデッドロックに陥らない経路を見つけることを目指している. こういった設定は PP や CBS を応用して解くことができる.

連続時間, 異種混合

MAPF は各エージェントが各タイムステップで同期して動くことを仮定しているが, これは少し窮屈な仮定で, グラフの辺によって移動時間を変えたい場合, 重み付きグラフ上での MAPF [Walker+ IJCAI-18] [Ren+ IROS-21] を考えることになる. グリッド上の任意の斜めの動きを許す Any-Angle MAPF [Yakovlev+ ICAPS-17] という設定もある. この方向の極限には, 連続時間で MAPF を解く設定が存在しており, Continuous MAPF [Andreychuk+ AIJ-22] と呼ばれる. 移動時間ではなく, エージェントの大きさがまちまちな設定は Large-Agents MAPF [Li+ AAAI-19] と呼ばれる. 移動時間やらエージェントの形状がバラバラになった極限にはマルチロボット・モーションプランニング (Multi-Robot Motion Planning; MRMP) [Solis+ RA-L-21] [Kottinger+ IROS-21] [Okumura+ IJCAI-23] という, 非常に難しい問題が待ち構えている.

その他

ざっくりと派生問題を見てきたが, 他にも, 複数ゴールを仮定する Multi-Goal MAPF [Surynek AAAI-21], 多目的関数の最適化を解く Multi-Objective MAPF [Ren+ RA-L-21] [Ren+ ICRA-21], エージェントが利己的な設定での MAPF [Amir+ AAAI-15], エージェントが途中で壊れるかもしれない設定 [Okumura+ AAAI-23] など, MAPF の派生問題は本当にたくさんあり, 毎年すごい勢いで誕生する.

手を動かしたい

文献紹介を追えて, このチュートリアルも締めくくりへと向かっていこう.

さらに興味がある人は, 実際に手を動かしてみないと分からないことはたくさんあるので, コードを触ってみることをお勧めする. 昨今の多くの研究者はコードを GitHub で公開しているので, それを漁っていくことになる. ただし MAPF は大規模な難しい問題であり, パフォーマンスを確保するために, たいていの場合は C++ が採用されている. したがって読みやすいわけではない.

幸いにも PIBT や LaCAM にはミニマムの Python 実装例が存在する. PP や CBS も実装は難しくないが, スケーラブルな実装にするには色々と苦難が待ち構えており, 性能が必要なら @Jiaoyang-Li や @Kei18 のコードから引っ張ってくるのが手っ取り早いと思う. 可視化ツールとしては mapf-visualizer が利用できる.

より深い文献

ここまで紹介したアルゴリズムの内容は, 2023年11月に行ったケンブリッジ大での講演に基づく.

Pathfinding for 10k agents - Wednesday Seminars, the Department of Computer Science and Technology, University of Cambridge, Nov. 2023. [リンク]

もう少し広く MAPF のことを知りたければ AAMAS-22 のチュートリアルの録画 が参考になるだろう. また, mapf.info というサイトがあり, 文献を漁ってみるのも良い.

関連する国際会議・ジャーナルも紹介しておこう. AAAI や IJCAI といったいわゆる General AI の会議にインパクトのある成果が報告されることが多いが, マルチエージェントを扱った AAMAS や AI プランニングに特化した ICAPS には面白い論文がたくさん登場する. 組合せ探索に関する SoCS という会議にはマニアックな論文がよく出る. もう少しロボティクスに寄せると ICRA や IROS になる. また, 非定期的に WoMAPF という MAPF に関するワークショップが開催されることもある. 論文誌としては AIJ や JAIR だが, これは完成度の高いワークが要求・掲載される. T-RO や RA-L といったロボティクスのジャーナルに投稿する人も多い.

もっと深くダイブしたいのであれば, 博士論文をどうぞ.

Okumura, K. “Planning, Execution, Representation, and Their Integration for Multiple Moving Agents.” PhD Dissertation at Tokyo Institute of Technology. 2023. [PDF]

締め

ざっくり MAPF の世界を見てきたが, MAPF が様々な応用をもつ魅力的な問題であり, 近年爆発的に研究が進んでいる という点が伝わっていると嬉しい. この分野はまだまだ発展途中であり, 特に LNS2 や LaCAM などのメタアルゴリズムが出てきたのはつい最近で, そのポテンシャルはまだ十分に引き出されていないと思う. 実世界への展開も含め, 研究すべきことはたくさんある.

仮に研究したい・デプロイしたいという人がいれば, 連絡もらえれば相談に乗ります.

引用

@article{okumura2024tutorial,
  title   = "マルチエージェント経路計画の紹介",
  author  = "Keisuke Okumura",
  journal = "kei18.github.io/note",
  year    = "2024",
  url     = "https://kei18.github.io/note/posts/mapf-tutorial"
}

あとがき